摘要
本项目:
- 设计了一个包含传热和对流两种物理现象的简单模型,该模型的形状尺寸参数和物理边界条件设置都可以在一定的范围内改变,
- 使用Star-CCM+的Design Manager功能进行sweep研究,
- 使用java编程和Design Manager的sweep功能,计算了183,750个算例,
- 将该模型的输入和输出数据保存成一个单独的数据集,
- 可以在后面的机器学习中进行试验,
- 最终通过对数据集进行机器学习,得到了一个神经网络模型,可以用来进行预测任意该模型在不同参数下的热表现。
- 验证了如果有足够的数据,就可以通过机器学习与工程应用结合进行研究,得出有价值的成果。
软硬件资源
软件:
- Star-CCM+
- 3D-CAD
- Automation
- Design Manager
- Java
- Jupyter Notebook
- pandas
- numpy
- matplotlib
- pytorch
硬件:
- PC
- 6核以上CPU
- 8G RAM
- 独立显卡
模型
模型如下图所示:
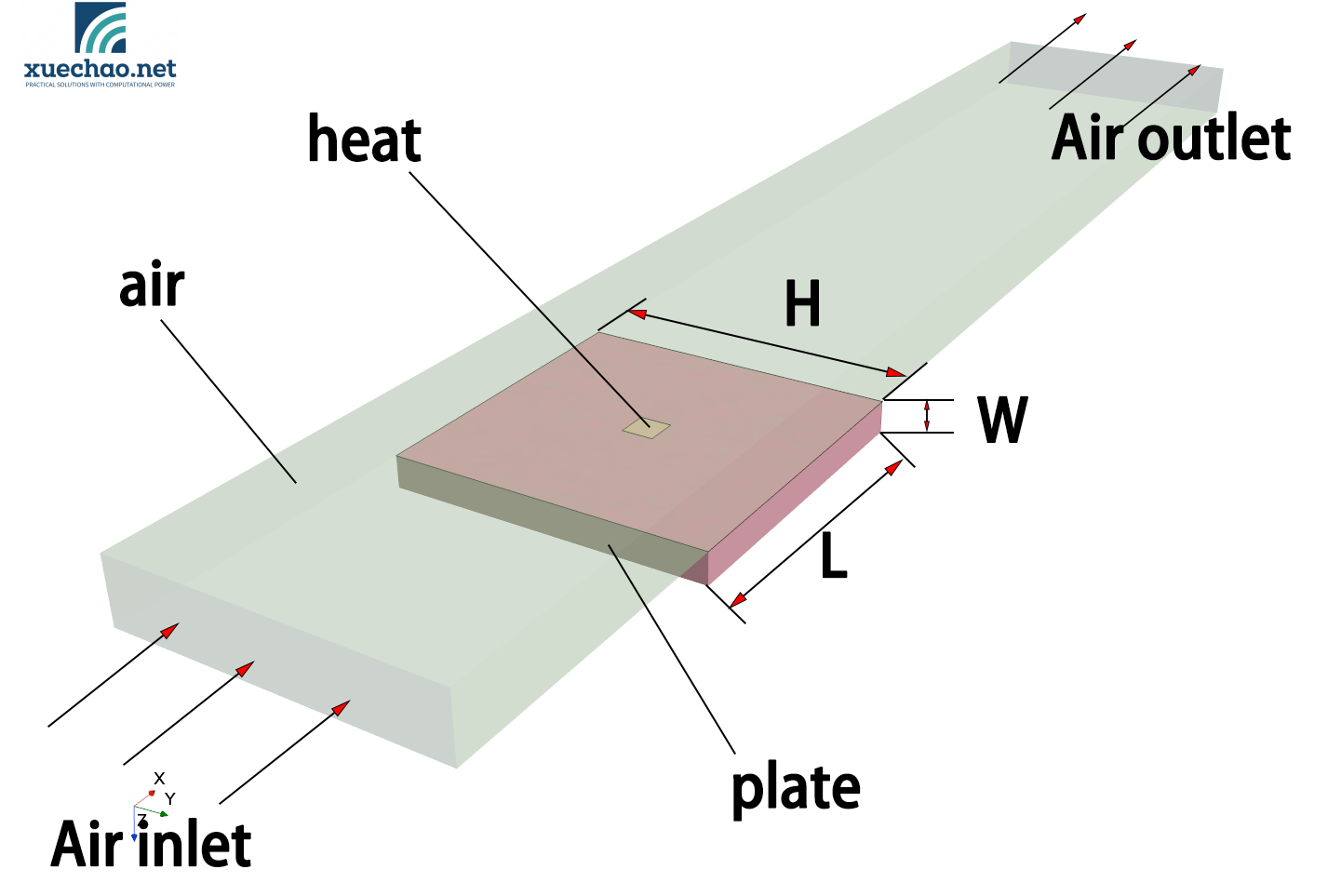
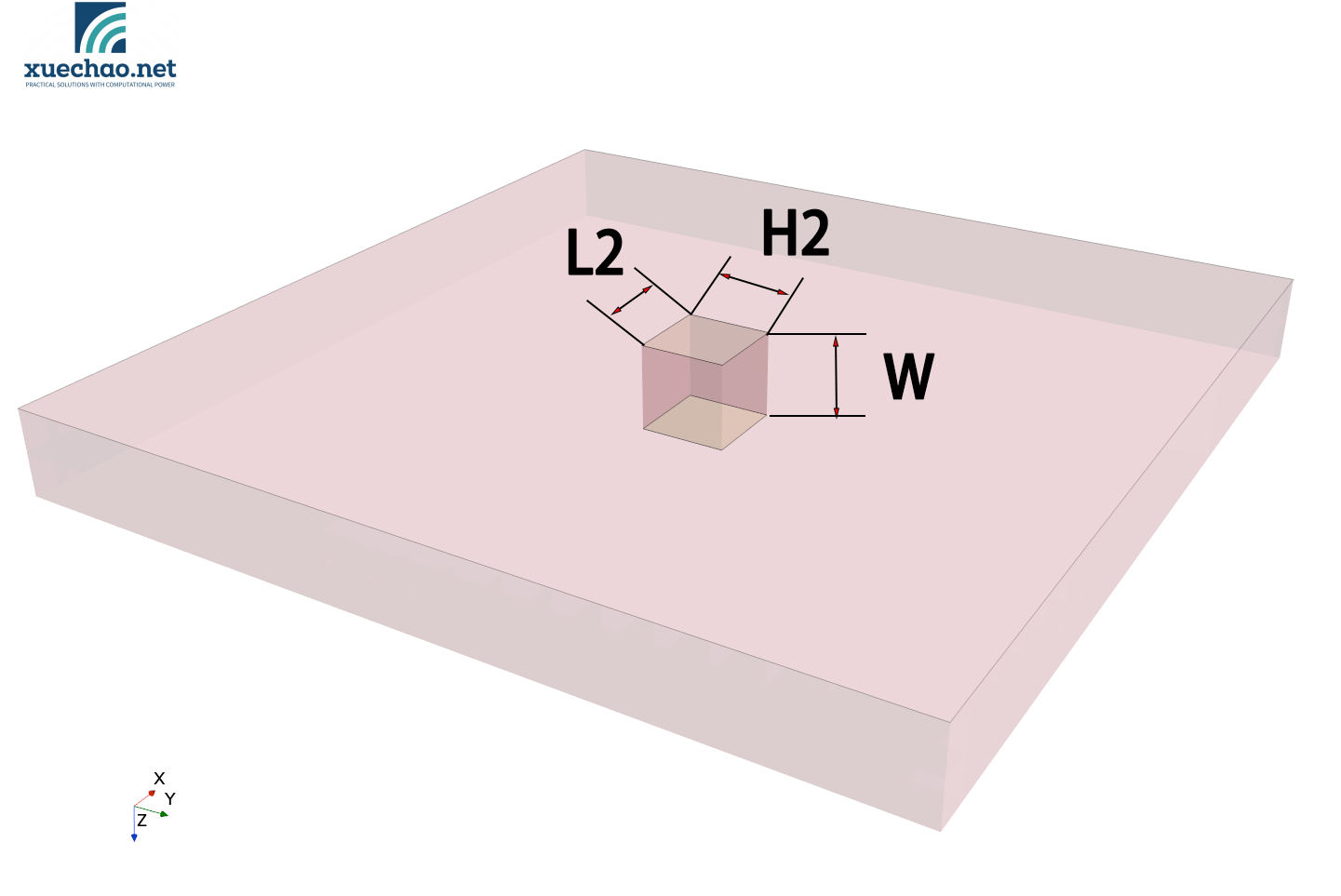
模型由3部分构成:
- heat
- plate
- air
heat:发热体,材料属性设置为铜,与plate紧密连接在一起,之间没有热阻。其长宽高分别是尺寸变量。
plate:不发热,材料属性设置为铁,其长宽为尺寸变量,其高度与heat保持一致。
air:流体域,进口速度为变量,温度为恒定。
该简单的模型主要描述的就是从heat这个部件发出一定的热量,大部分通过与plate接触传到到plate上面,然后经过plate与air的对流换热散发到air中去,heat还有较少部分热量通过heat顶面与air直接对流换热。
该换热模型的变量一共有如下7个:
- H ——plate的宽,范围为[50,150]mm
- L ——plate的长,范围为[50,150]mm
- W ——plate的厚,范围为[5,20]mm
- H2 ——heat的宽,范围为[5,20]mm
- L2 ——heat的长,范围为[5,20]mm
- v_air ——空气的进口速度,范围为[5,20]m/s
- heat ——heat的发热量,范围为[1,20]w
数据集
该数据集可以在如下地址下载。
该数据集的名称解释如下:
- Design# :Star-CCM+中的设计编号
- “Name” :Star-CCM+中的DM单次计算顺序
- “T_d” :空气的进出口温差
- “T_inlet (C)” :空气进口温度
- “T_outlet (C)” :空气出口温度
- “energy_out” :根据空气进出口温差计算的空气通过对流带走的热量
- “heatT (C)” :heat的平均温度
- “mass (kg/s)” :空气的质量流量
- “Performance” :DM对单次设计的性能评价,我们只是通过Sweep功能来收集数据,该项没有意义。
- “H (mm)” :plate的宽
- “H2 (mm)” :heat的宽
- “L (mm)” :plate的长
- “L2 (mm)” :heat的长
- “W (mm)” :plate的厚
- “Wair (mm)” :为模型中air的高度,设置为常量
- “heat” :heat的发热量
- “v”:空气的进口速度
机器学习
将数据集导入notebook并且做一些处理,选取我们主要的输入和输出:
df.columns
Index(['Design#', 'Name', 'T_d', 'T_inlet(C)', 'T_outlet(C)', 'energy_out',
'heatT(C)', 'mass(kg/s)', 'Performance', 'H(mm)', 'H2(mm)', 'L(mm)',
'L2(mm)', 'W(mm)', 'Wair(mm)', 'heat', 'v'],
dtype='object')
selected_columns = [ 'H(mm)', 'H2(mm)', 'L(mm)','L2(mm)', 'W(mm)', 'heat', 'v','heatT(C)']
df =df[selected_columns]
df.head()
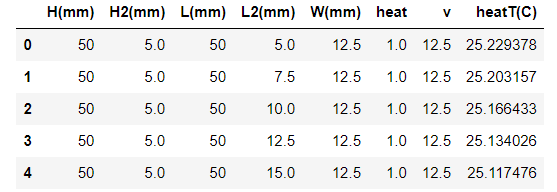
df.describe()
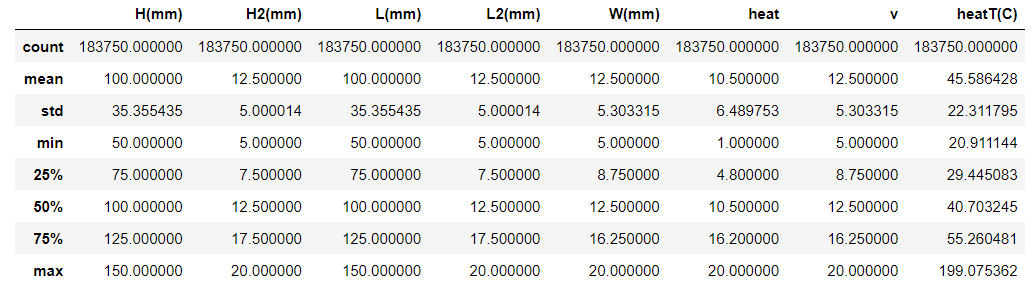
数据集数据之间的线性相关性如下图所示:
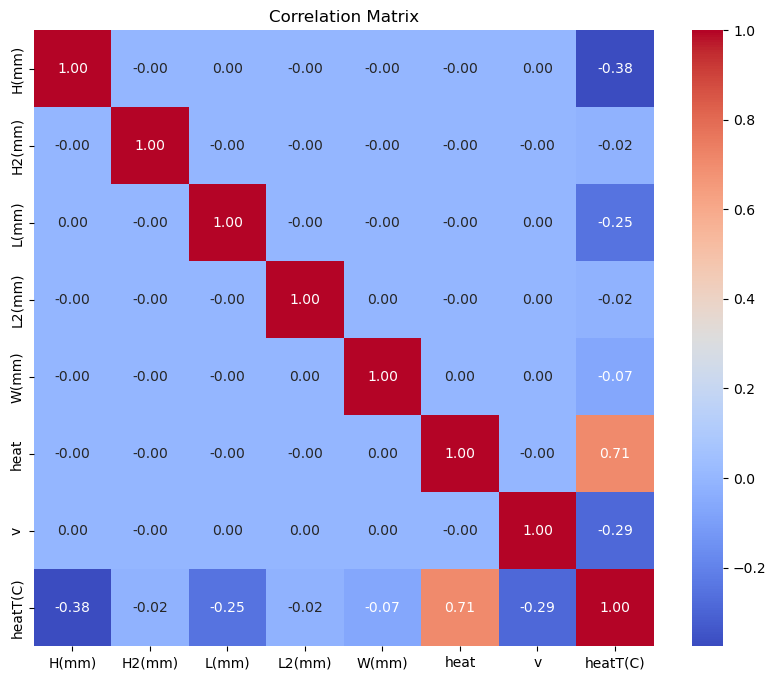
使用SK-learn线性拟合:
model=LinearRegression()
model.fit(X_train,y_train)
测试集中,其预测值与实际值的对应关系如下:
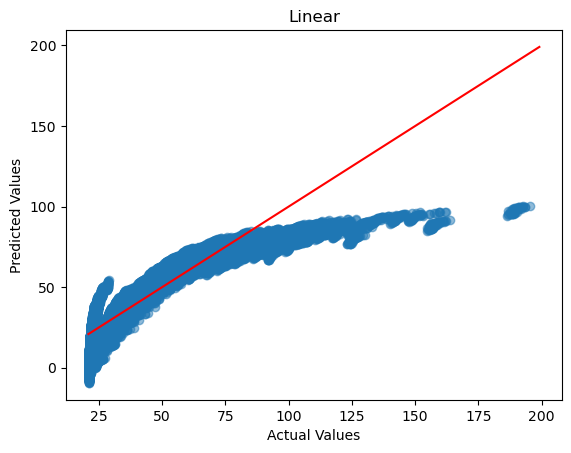
测试集的预测准确性评价如下:
R2 score: 0.7899667696453285
Mean Squared Error: 104.53257228500799
Mean Absolute Error: 6.8060228938554435
使用神经网络进行学习:
神经网络模型主要采用了线性连接和ReLU激活函数。
- 神经网络结构为1个输入层,7个隐藏层,1个输出层;
- 通过多个隐藏层,和每个隐藏层足够多的神经元,可以拟合比较复杂的物理现象;
- 通过使用ReLU激活函数,我们可以模拟传热和对流过程中的非线性现象。
def create_model_more_hidden_layers(num_input_cols,num_output_cols):
model=nn.Sequential(
nn.Linear(num_input_cols,10),
nn.ReLU(),
nn.Linear(10,50),
nn.ReLU(),
nn.Linear(50,100),
nn.ReLU(),
nn.Linear(100,100),
nn.ReLU(),
nn.Linear(100,100),
nn.ReLU(),
nn.Linear(100,100),
nn.ReLU(),
nn.Linear(100,50),
nn.ReLU(),
nn.Linear(50,10),
nn.ReLU(),
nn.Linear(10,num_output_cols) # Output Layer with 1 neuron
)
return model
num_input_cols = X_train.shape[1]
num_output_cols=1
num_epochs=10000
learning_rate=0.0001
model= create_model_more_hidden_layers(num_input_cols,num_output_cols).to(device)
train_test_model(model,X_train,y_train,X_test,y_test,num_epochs,learning_rate)
测试集中,其预测值与实际值的对应关系如下:
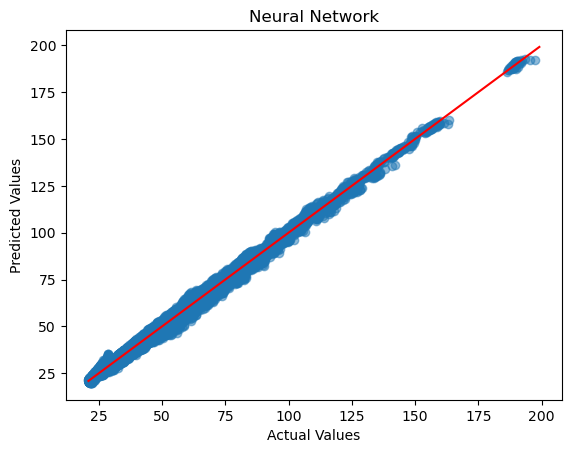
测试集的预测准确性评价如下:
R2 score: 0.9957430057650765
Mean Squared Error: 2.1337025
Mean Absolute Error: 1.0782065
结论
通过以上一个简单传热和对流模型的整个研究过程,可以看出,在采用神经网络进行机器学习可以训练出来很好的模型用于预测复杂的物理现象。
虽然本项目使用的数据是通过大量的计算得到的,但是通过仿真获得大量数据进行机器学习也有以下重要意义:
-
数据丰富性:仿真可以生成大量多样化的数据,这对于训练复杂的机器学习模型尤为重要,尤其是在实际数据稀缺或获取成本高的情况下。
-
成本效益:相比于现实中收集数据的高昂成本,仿真数据的生成成本通常较低,而且可以在较短时间内生成大量数据。
-
可控性:仿真环境下可以精确控制变量,方便研究特定条件对模型表现的影响,有助于模型的优化和验证。
-
覆盖极端情况:仿真可以模拟现实中难以遇到的极端情况,为机器学习模型提供全面的训练数据,提高模型在各种情况下的表现。
进一步的思考
- 已经验证了通过大量反映模型特征的数据进行机器学习行成整个闭环,我们可以利用任何我们积累的工程数据,通过机器学习来进行重新认识和解读,甚至可以训练机器模型用于新的优化设计计算。
- 这个简单的模型非常简单,整体网格量也非常少,计算这大约18万组数据消耗的时间大约2-3周。如果一个更为复杂的模型,网格量稍微多一点,单个case计算时间以十几分钟计的话,那么是不是不可能得到一个如此巨大的数据集?
