摘要
在前面文章中介绍了本研究的模型,在本章中:
- 为了从最基础,最简化的角度来进行探索,选取模型8个可变化的参数中的1个作为变量进行研究,
- 同时为了研究变量在不同的取值范围的表现,约定了不同的取值范围,
- 使用sweep计算来获得数据集,
- 希望通过对该模型描述的物理现象出发,对数据集进行基于物理理解的分析,
- 然后再进行机器学习,使用不同的模型进行拟合,
- 来评估不同回归模型在不同数据集下的表现。
模型
模型在上篇文章已经做过介绍,如下图所示:
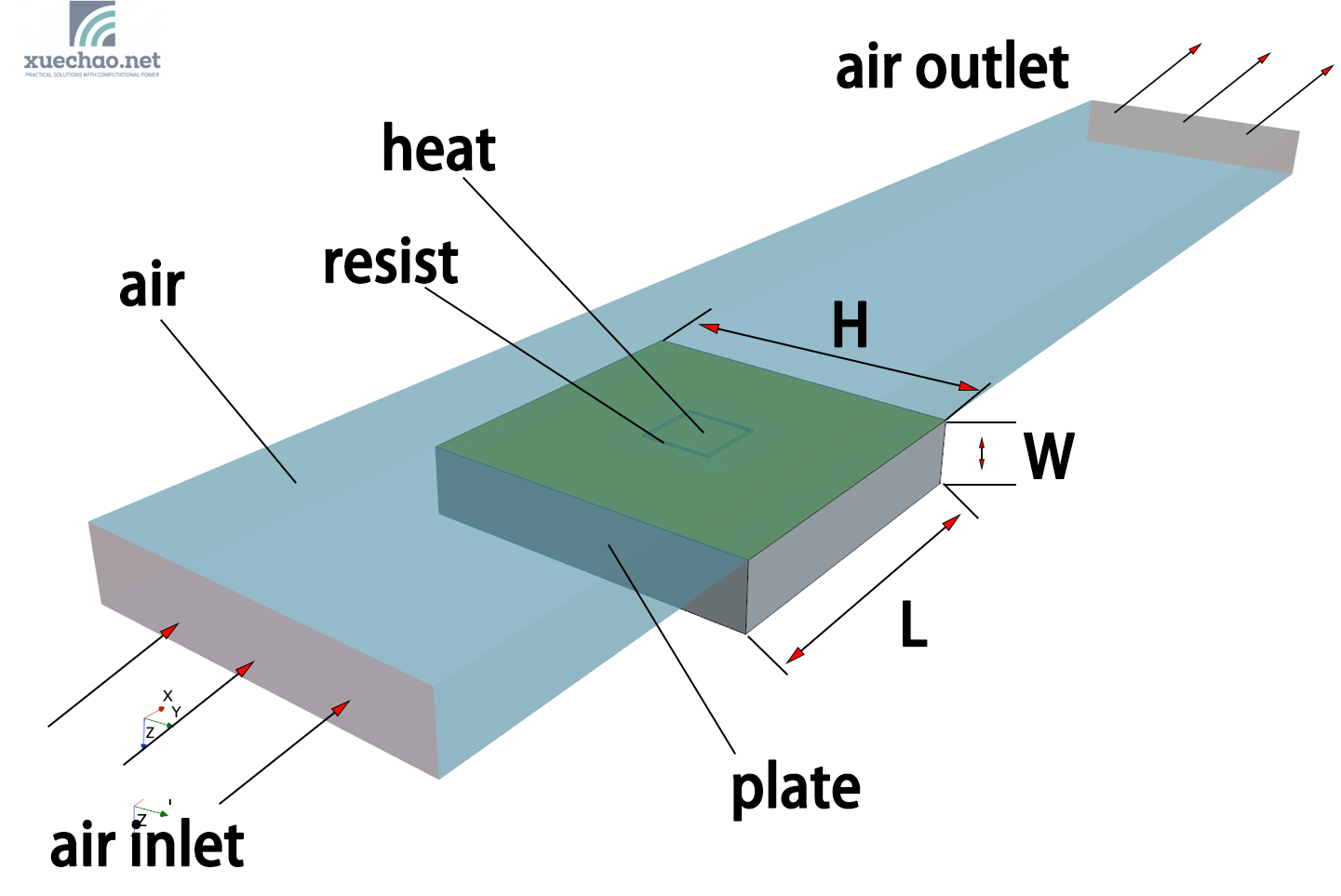
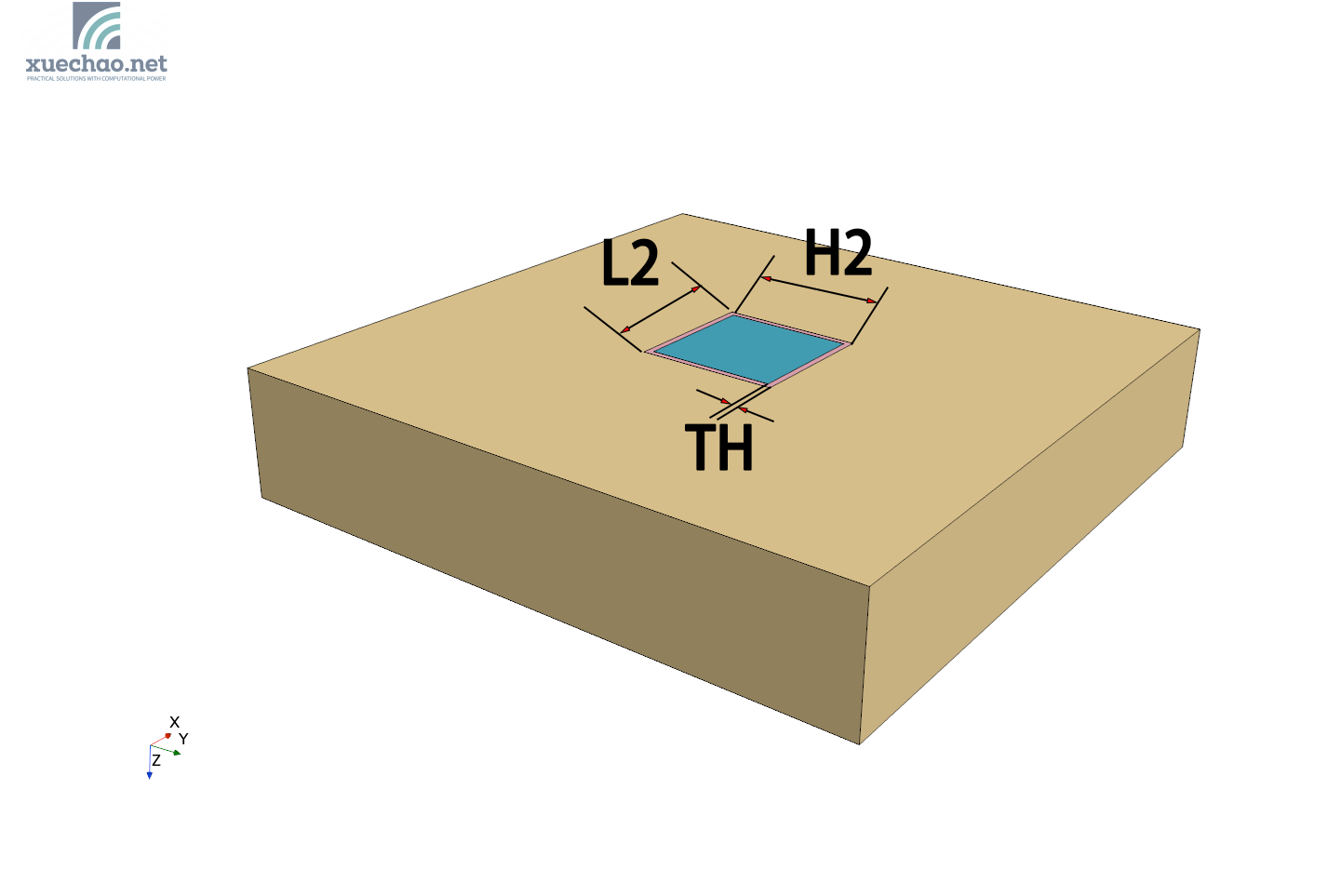
该换热模型的可变参数一共有如下8个:
- H ——plate的宽,
- L ——plate的长,
- W ——plate的厚,
- H2 ——heat的宽,
- L2 ——heat的长,
- TH ——resist的厚,
- v_air ——空气的进口速度,
- heat ——heat的发热量。
单变量研究
在本章中,我们只选取一个参数作为变量,其他的参数为恒定值。该模型的截面如下图所示:
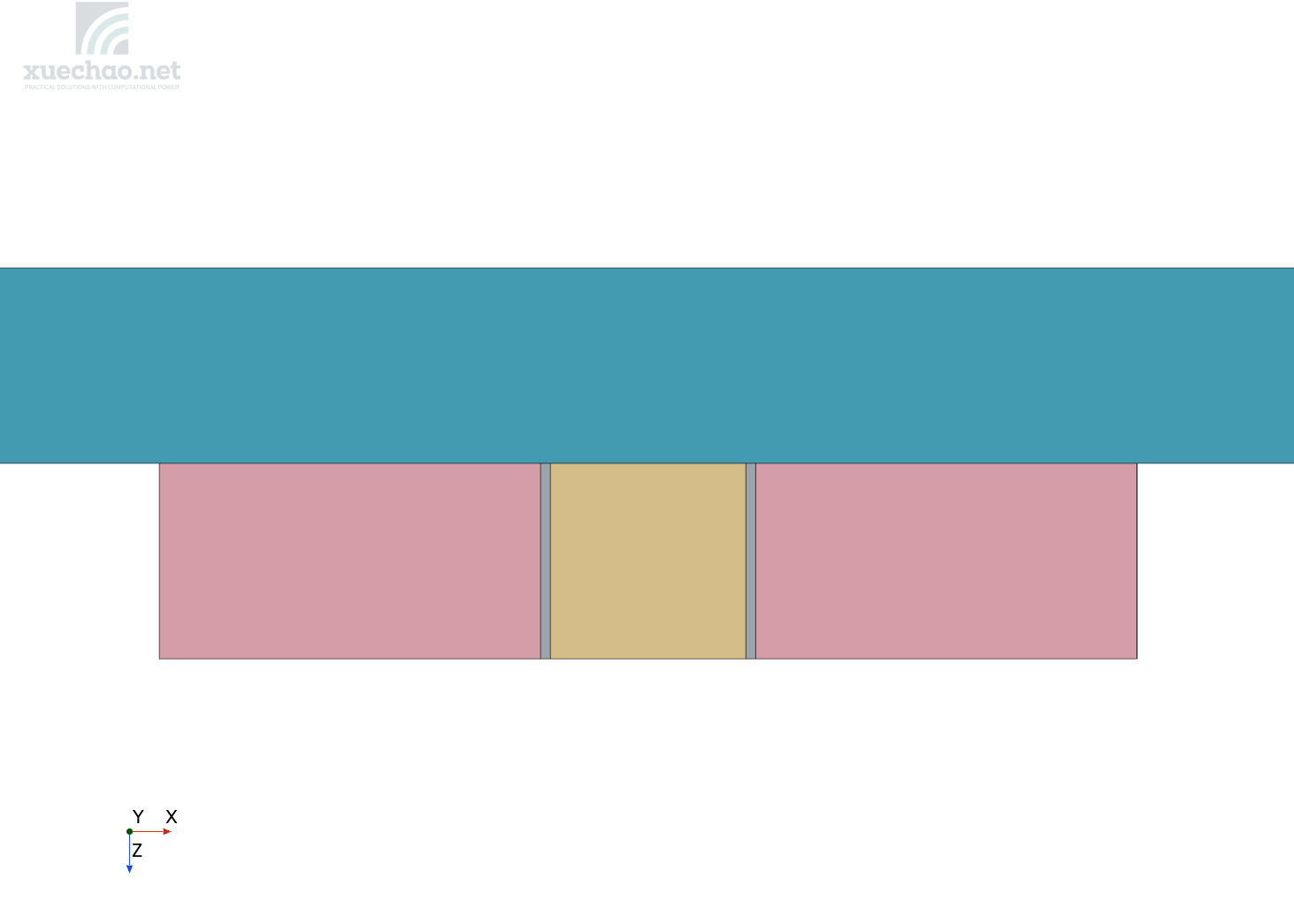
该模型所反映的物理现象我们上个文章已经介绍:“从heat这个部件发出一定的热量,大部分热量首先经过具有较小导热系数的resist,传递到plate上面,然后经过plate与air的对流换热散发到air中去,heat还有较少部分热量通过heat顶面与air直接对流换热。”
如果忽略resist部件与空气的对流交换,以及忽略一些三维传热,并且假设heat部件温度均布(由于该部件的导热率非常大),我们使用热路图来表示这个模型的传热过程,如下图所示:
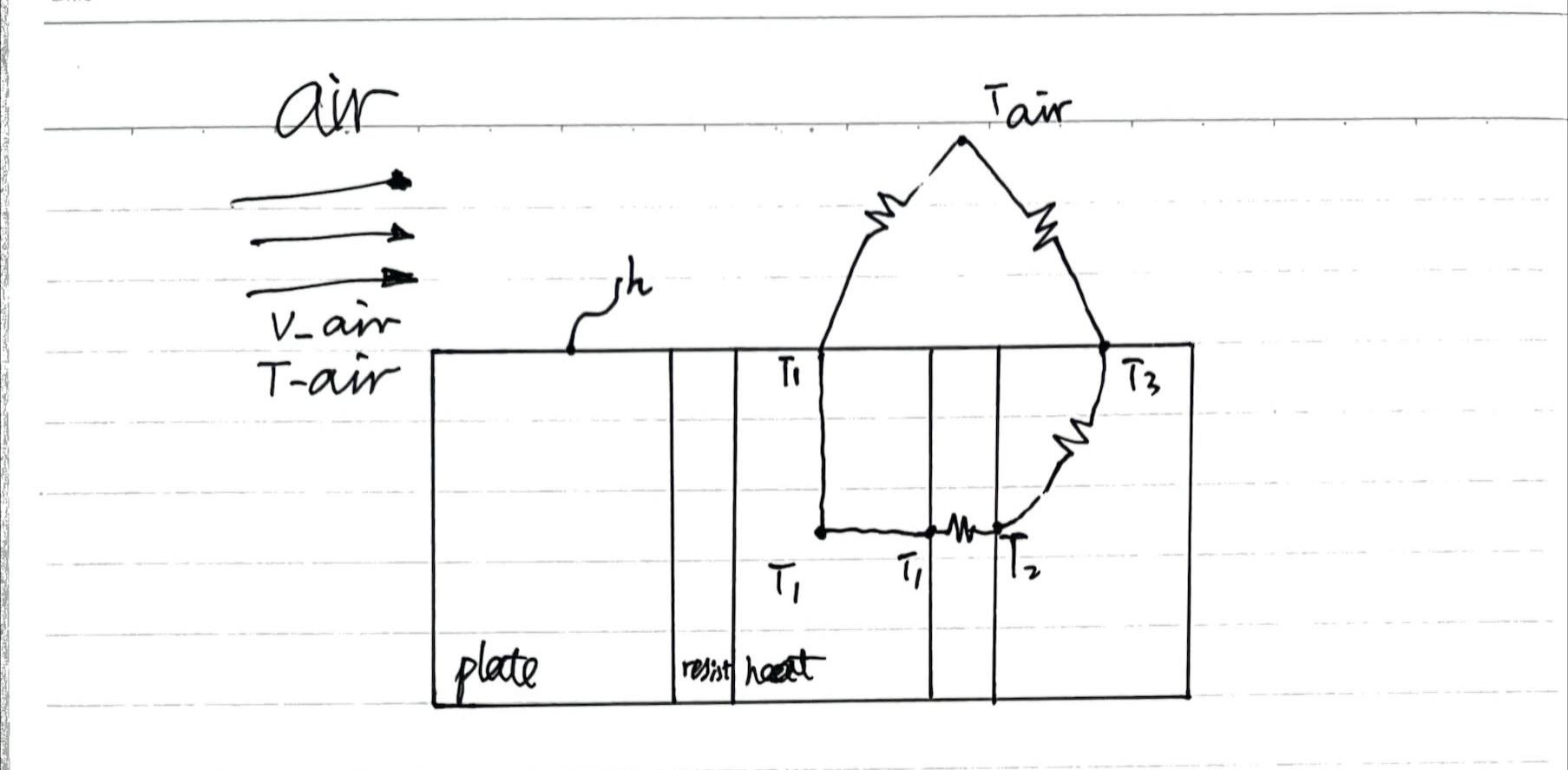
v_air作为变量的研究
首先,我们将空气的速度v_air作为变量进行研究。根据上面的热路图,v_air的改变,主要影响了空气与固体的对流换热系数,根据牛顿冷却定律:Q = h * A * (Ts - Tf),物体表面的温度与对流换热系数的倒数,既1/h成正比。
使用软件计算该模型在不同空气流速下的情况,heat部件的温度与空气速度有如下关系:
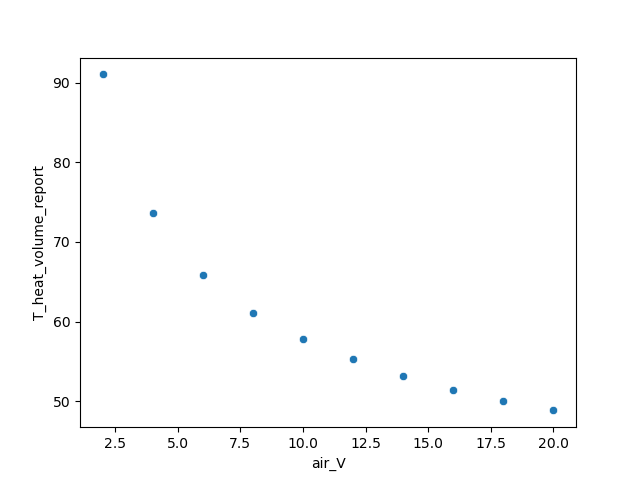
上图反映的是空气的速度在[2.5,20]m/s的范围内,heat部件的平均温度的变化。在这个关系中,我们明显看出来我们最开始利用牛顿冷却定律的分析是与仿真结果吻合的。随着空气速度的增大,空气与固体的对流换热系数也增加,进而其倒数变小,最终使得heat部件的温度呈现一种非线性的反比例关系。
如果空气速度范围为[8,12]m/s,heat部件的温度变化如下图所示:
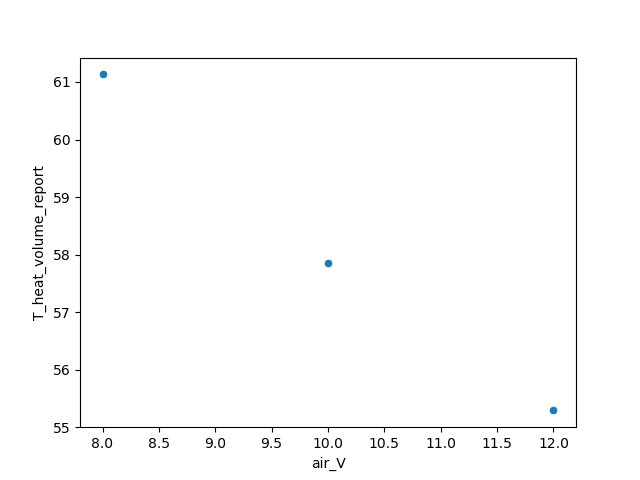
从上面可以看出,一个变量在不同的取值范围内,该变量与结果变量之间的线性关系强烈程度是不同的。
heat部件的横向位置作为变量的研究
上面我们看了热点温度和冷却空气的关系,呈现了反比例关系,为了产生更为复杂的数据,我们在原始模型上增加了一个变量,D,用来描述heat部件的横向位置,如下图红圈处所示:
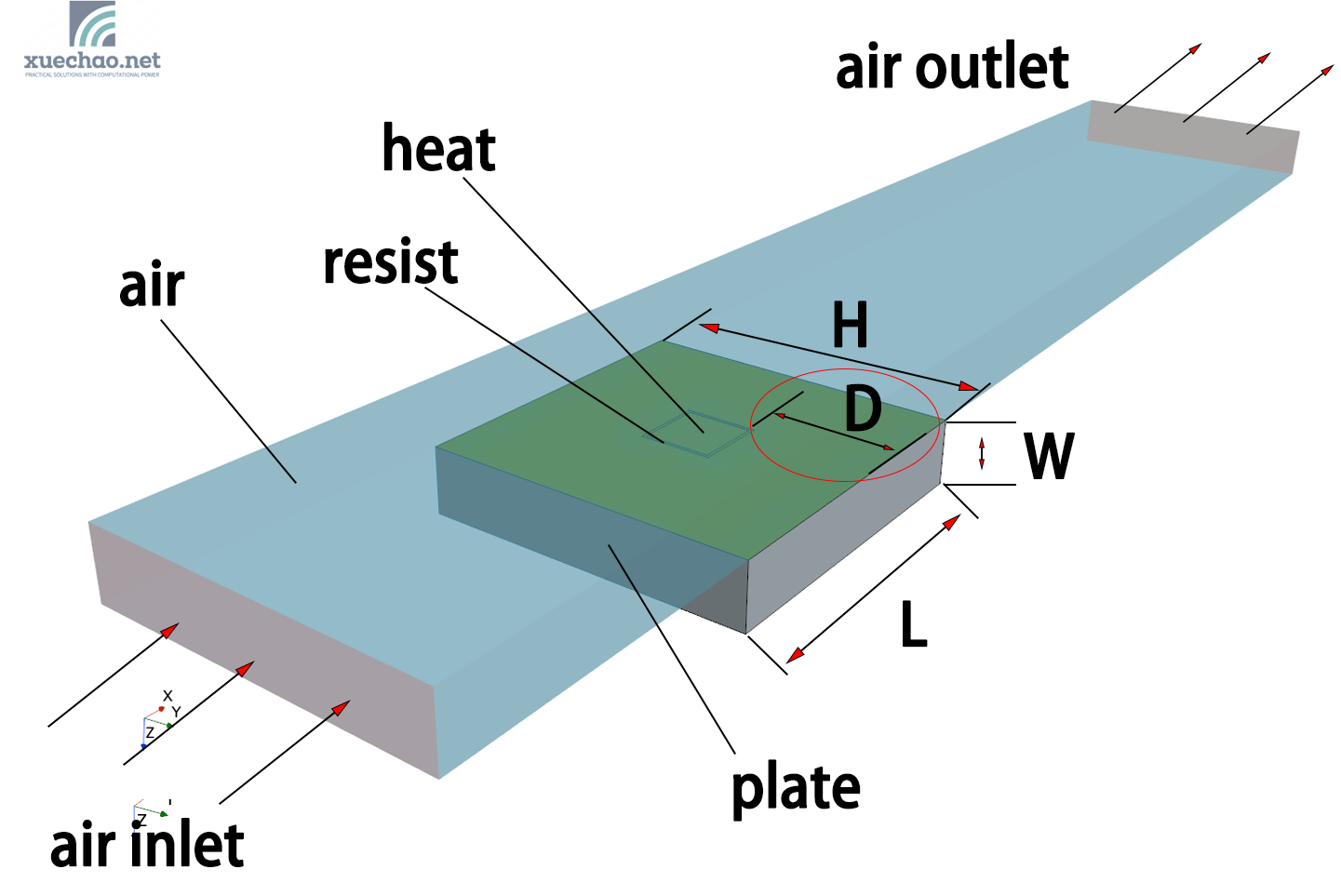
既heat部件在垂直于冷却空气流速的方向上有一个位置变化,其距离plate的侧边的距离为D,下图为3个不同的D的模型的示意图。
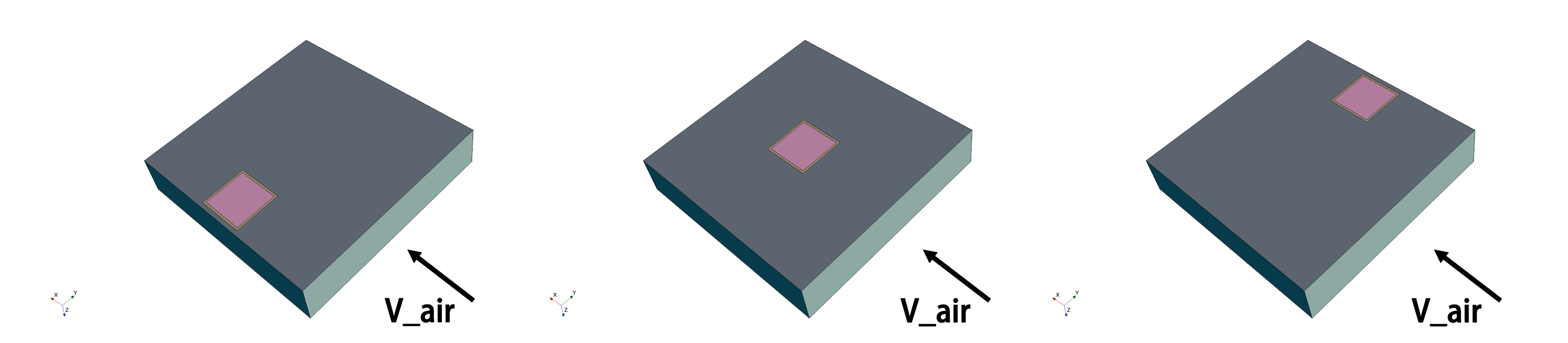
我们只将该模型中D作为唯一的变量,其他的参数保持不变,计算了多个不同D的案例,最终形成了相应的数据集。
heat部件的温度与D的关系如下图所示:
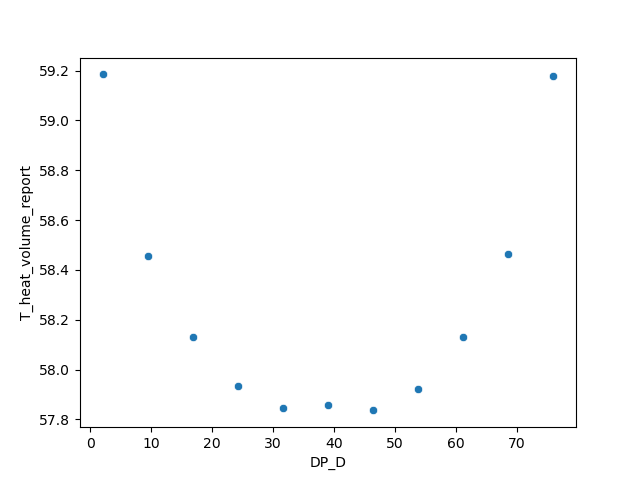
在该模型中,只有参数D为变量,影响heat部件的温度的主要因素是D的大小,既heat部件的相对位置。如果heat部件的位置比较靠近边缘,那么从下图截面的温度分布我们可以看出,heat部件的有一侧比较靠近边缘,其与plate的换热受该侧plate的温度分布梯度影响,从而造成该侧的导热效果的降低,进而推高了heat部件的温度。

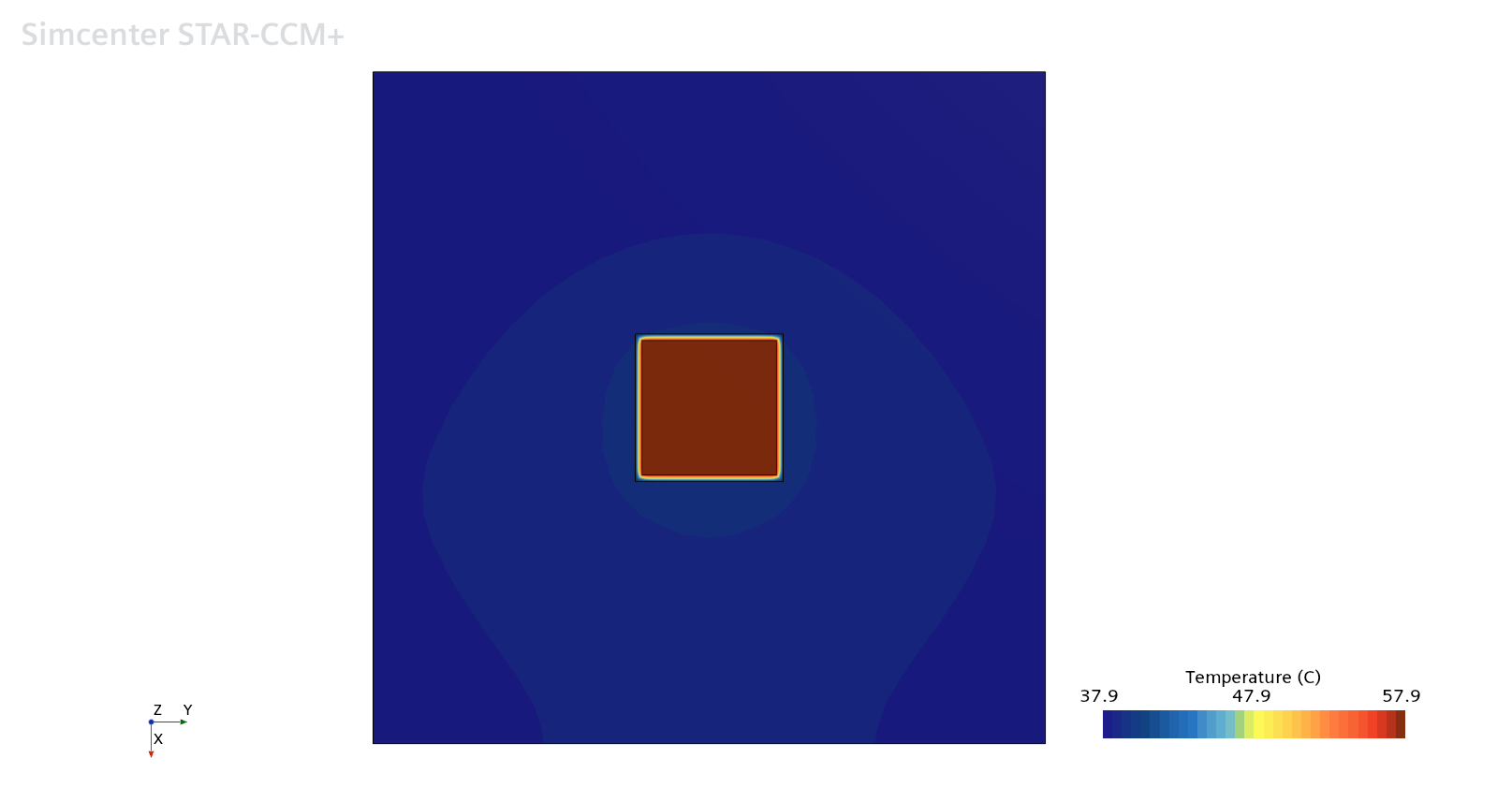
随着D的逐渐增大,heat部件向中间移动,改善了其侧面的传热能力,因此heat部件位于中间位置的时候,其温度最低。下图为heat部件位于中间位置的温度分布图。
heat部件的横向位置作为变量的数据集的机器学习研究
Scikit-learn线性回归
首先我们利用Scikit-learn的线性拟合方法对该数据集进行拟合,首先要强调的是,我们已经知道参数D与heat部件的温度T之间不是线性关系。但是,我们还是试一试。
model=LinearRegression()
model.fit(X_train,y_train)
我们使用该参数作为变量通过CFD软件扫描计算得到的数据集作为研究对象,使用SK-learn的线性回归进行训练,其训练模型预测的准确度如下图所示:
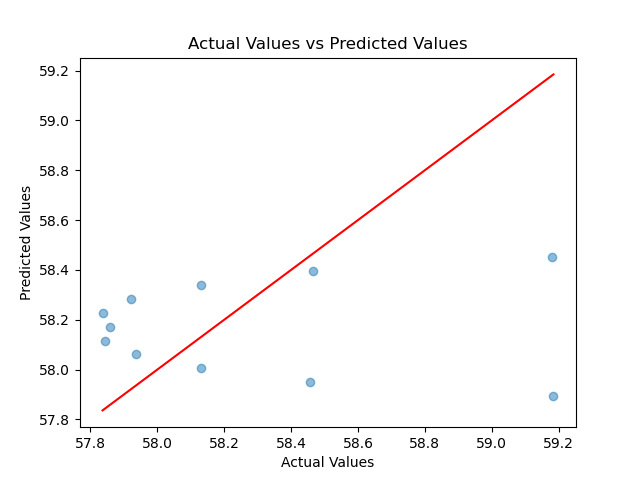
其真实结果和预测结果的D vs T分布如下图所示:
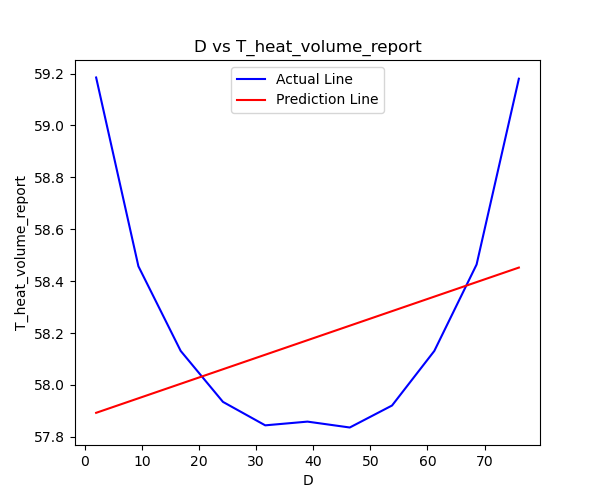
我们可以明确的看出,由于该模型从物理现象的角度,D和T的关系是非线性的,因此不能使用线性拟合来进行训练数据。
Scikit-learn多项式回归
由于从物理现象我们已经得知,D和T的关系不是线性关系,我们从上面的结果可以看出,D和T大概是一个抛物线形式的关系,那我们可以利用Scikit-learn的多项式回归对该数据集进行训练。
首先我们使用2阶的多项式,因为我们刚刚猜测D和T的关系大概是抛物线的关系。
model = make_pipeline(PolynomialFeatures(degree=2), LinearRegression())
model.fit(X_train,y_train)
其训练模型预测的准确度如下图所示:
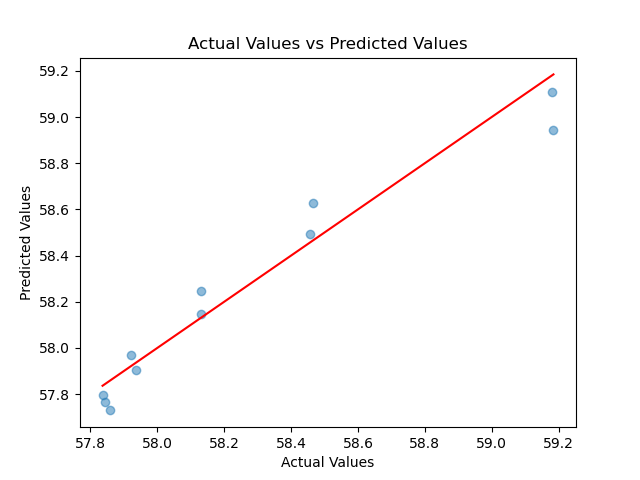
其真实结果和预测结果的D vs T分布如下图所示:
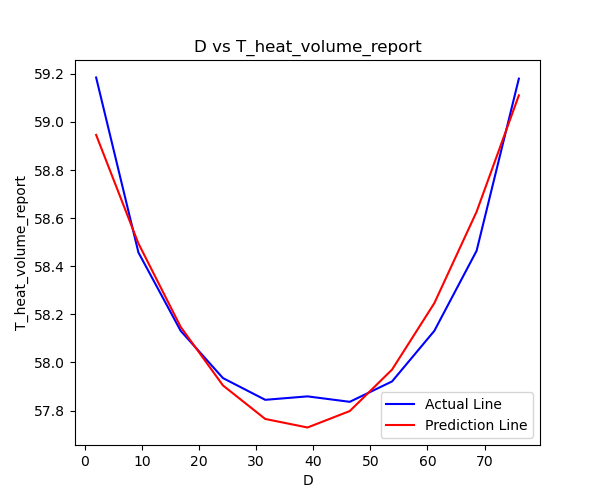
哇哦,使用2阶多项式回归的效果比线性回归要好的多。但是还是有一点误差。那么我们试试增加多项式的阶数。
3阶多项式回归训练模型预测的准确度如下图所示:
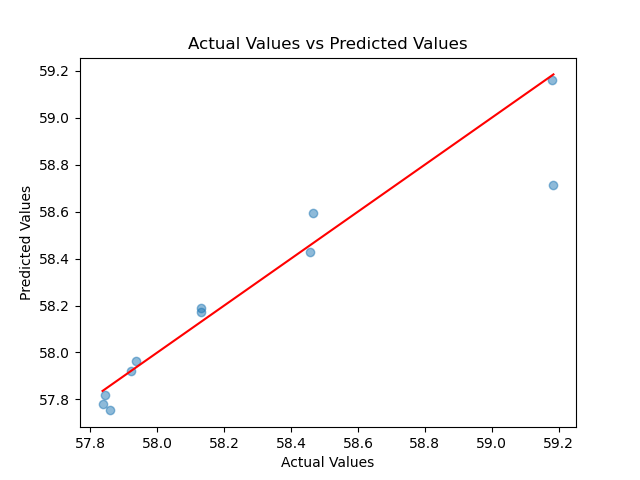
其真实结果和预测结果的D vs T分布如下图所示:
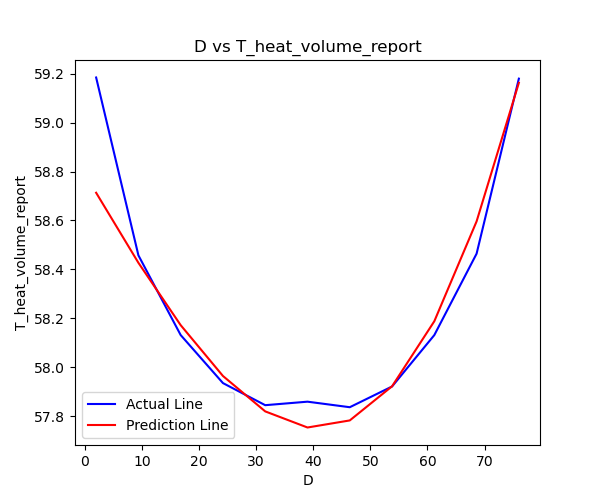
使用3阶多项式回归的效果比2阶多项式回归要好。
4阶多项式回归训练模型预测的准确度如下图所示:
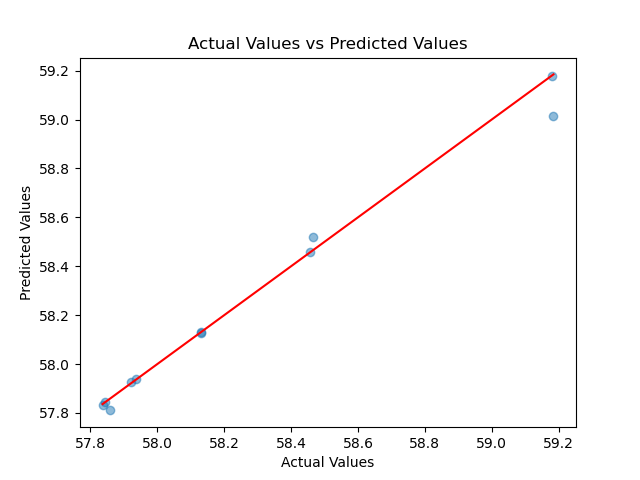
其真实结果和预测结果的D vs T分布如下图所示:
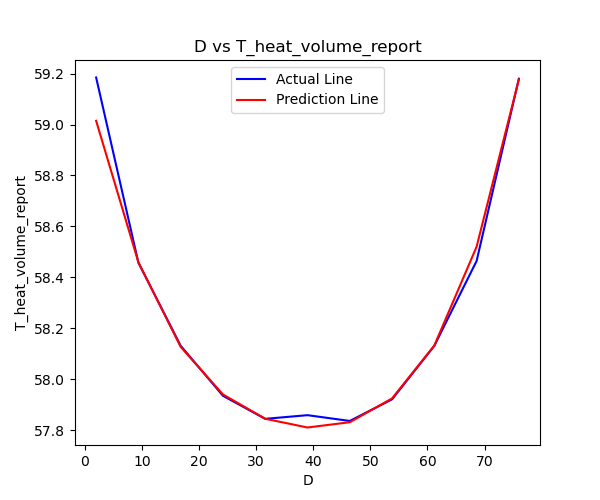
从上面的图可以看出,使用4阶多项式回归的效果已经非常好了。
结论
本章通过对一个稍微复杂一点的传热和对流模型中的一个参数作为变量,分别进行了两条路线的研究:
- 首先,从物理现象出发,以传热和对流换热理论为出发点,对变量和结果之间的相互关系进行了研究;
- 其次,使用机器学习的方法,以数据为出发点,使用简单的线性回归和多项式回归对数据集进行研究;
- 如果能够对物理现象有足够多认识的话,可以对我们选用机器学习模型的时候有很大的帮助,能够提高机器学习的准确度。
接下来,在第3章中,我们准备使用神经网络,对该数据集进行研究,并且与多项式回归进行一个对比。
