摘要
在前面文章中介绍了本研究的模型在使用SK-Learn模型的准确度,在本章中:
- 对上个章节中的数据集使用神经网络进行拟合,
- 将结果与SK-learn的结果进行了对比,
- 评估了神经网络模型在该数据集下的表现。
模型
模型在上篇文章已经做过介绍。
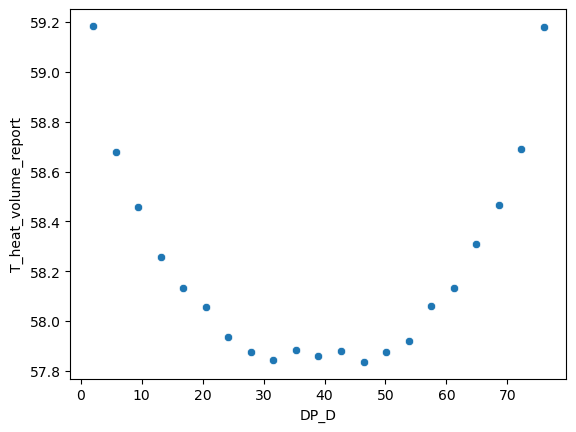
在之前的文章中,只选取一个参数作为变量,其他的参数为恒定值。我们在原始模型上增加了一个变量,D,用来描述heat部件的横向位置。为了更加适应神经网络模型对于数据集的要求,我们选用了包含21个计算结果结果的数据集。
heat部件的温度与D的关系如下图所示:
神经网络研究
在之前的文章,既“CFD与机器学习(1)一个简单的模型”,我们使用了一个‘神经网络结构为1个输入层,7个隐藏层,1个输出层’,该神经网络很好的拟合了一个模型用于处理我们的那个简单的模型的物理现象。
那么,神经网络的结构是该如何确定呢?一共要多少个层才算合适?每个层该如何确定神经元的个数呢?在工程领域,比如我们这个稍微复杂一点的传热模型所使用的变量该如何选择神经网络的结构呢?
我们会在后面的章节中进行探索,试图得到一点点对于工程数据使用神经网络的一点心得。
sk-learn多项式回归
前一章我们使用了4阶多项式回归训练模型预测的效果非常好,其准确度如下图所示:
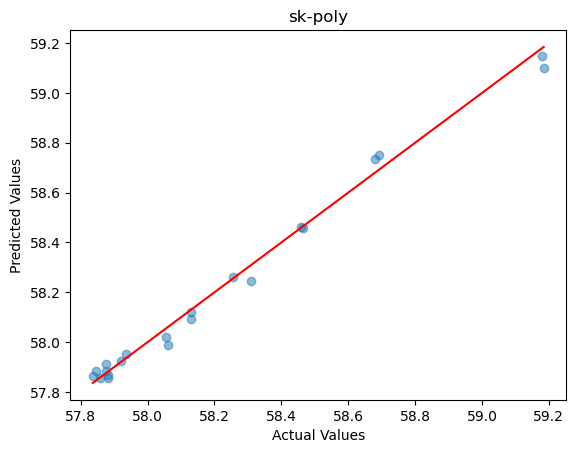
其真实结果和预测结果的D vs T分布如下图所示:
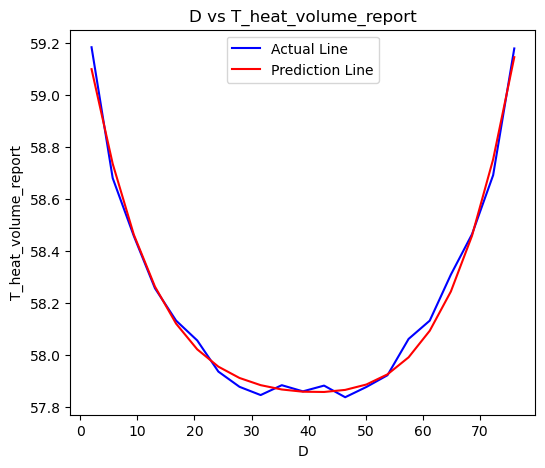
神经网络
我们然后使用神经网络进行一下拟合。神经网络模型主要采用了线性连接和ReLU激活函数。通过引入激活函数来模拟非线性的现象。
我们使用一个之前的那个神经网络,既有7个隐藏层的神经网络对同样的数据集进行训练和预测。其准确度如下图所示:
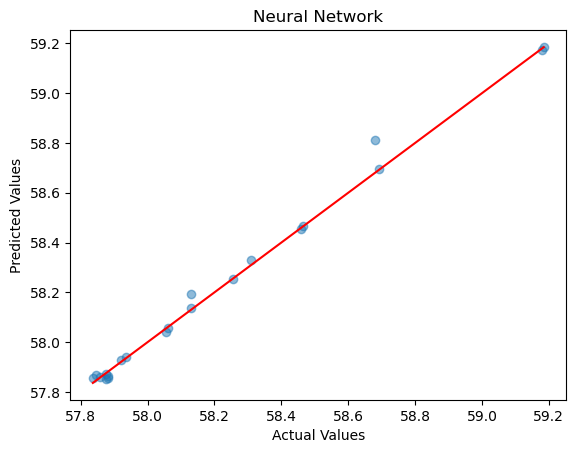
其真实结果和预测结果的D vs T分布如下图所示:
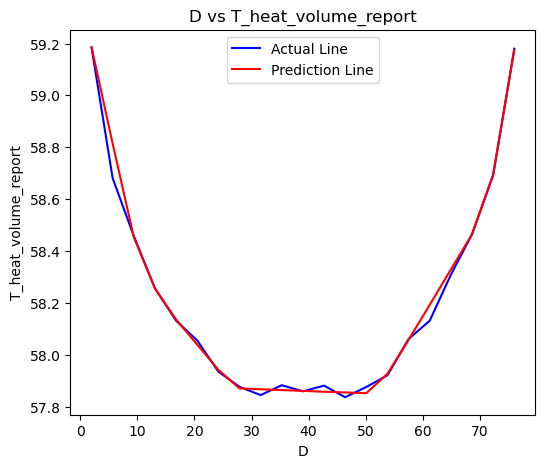
我们可以看出,神经网络在该数据集下的表现也非常好。
结论
本章通过对一个稍微复杂一点的传热和对流模型中的一个参数作为变量,我们使用神经网络,对该数据集进行研究,并且与多项式回归进行一个对比。可以看出神经网络的回归精度也是非常高的。一个足够复杂的神经网络可以模拟出来足够复杂的物理现象。
在下一章中,我们准备对比一下多项式回归和神经网络对于数据集大小要求的研究。
