Abstract
In the previous article, it was introduced that both SK-Learn polynomial regression and neural networks can yield good results for the model used in this study. However, it is generally believed that neural networks require larger datasets. In this chapter:
- Different-sized datasets are generated using CFD (Computational Fluid Dynamics) and fitted using both methods.
- The performance of polynomial regression and neural network models is evaluated on different datasets.
Dataset
Previously, we selected a dataset containing 21 computed results. We can adjust the step size of D to generate more datasets. For example, we can create a dataset with 11 data points or another with 101 data points, among other possibilities.
In the dataset with 11 data points, the relationship between the temperature of the heat component and D is shown in the figure below:
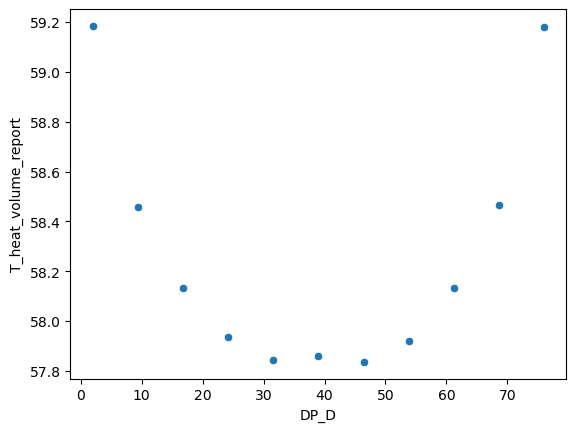
In the dataset with 101 data points, the relationship between the temperature of the heat component and D is shown in the figure below:
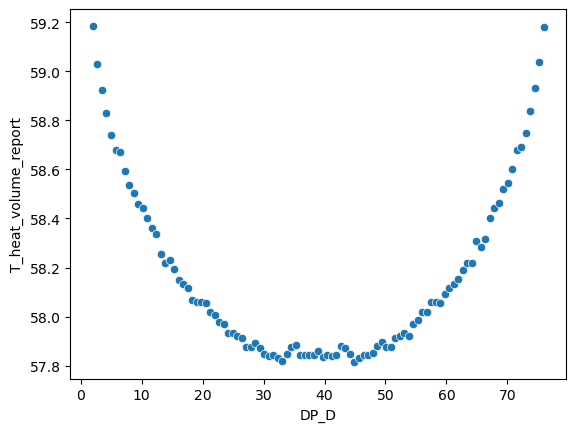
In the dataset with 371 data points, the relationship between the temperature of the heat component and D is shown in the figure below:
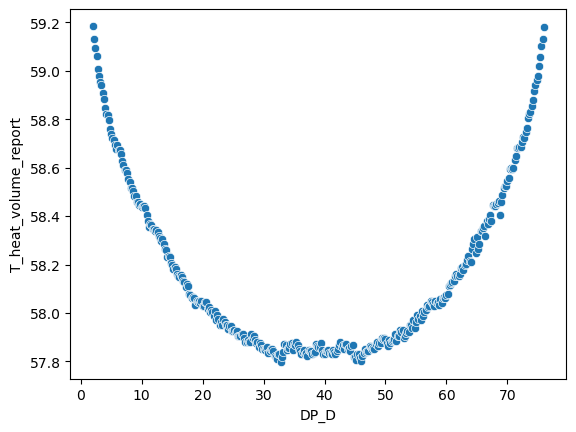
Dataset11
Dataset11 Polynomial Regression
A 4th-degree polynomial regression model was used for training, and the prediction accuracy on the test set is shown in the figure below:
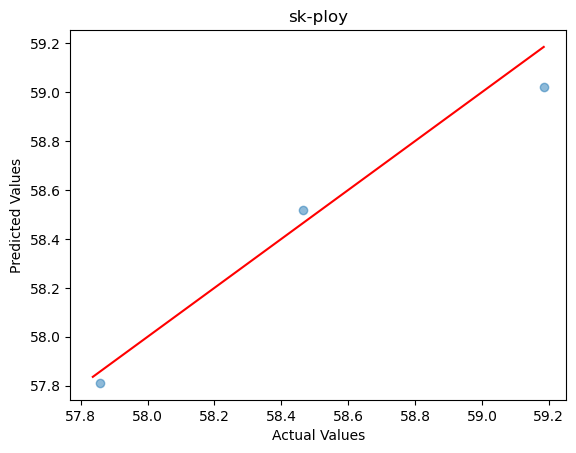
R2 score: 0.9628717222035422
Mean Squared Error: 0.010903528174133134
Mean Absolute Error: 0.0893634062848226
Dataset11 Neural Network
The same 7-layer hidden neural network model used in the previous article was applied, and the prediction accuracy on the test set is shown in the figure below:
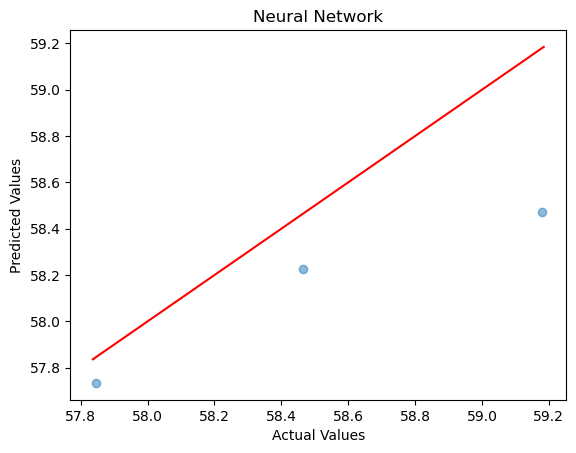
R2 score: 0.35997135381363976
Mean Squared Error: 0.19054323
Mean Absolute Error: 0.3524933
Dataset21
Dataset21 Polynomial Regression
A 4th-degree polynomial regression model was used for training, and the prediction accuracy on the test set is shown in the figure below:
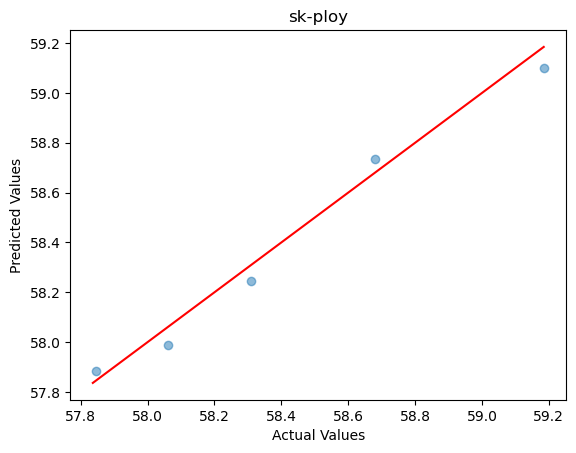
R2 score: 0.9814169221431929
Mean Squared Error: 0.004181097720090528
Mean Absolute Error: 0.06277254235435378
Dataset21 Neural Network
The same 7-layer hidden neural network model used in the previous article was applied, and the prediction accuracy on the test set is shown in the figure below:
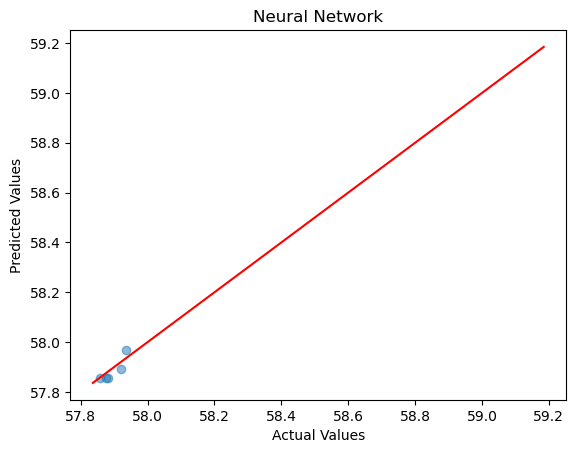
R2 score: 0.22970822906625143
Mean Squared Error: 0.00063205796
Mean Absolute Error: 0.02298813
Dataset38
Dataset38 Polynomial Regression
A 4th-degree polynomial regression model was used for training, and the prediction accuracy on the test set is shown in the figure below:
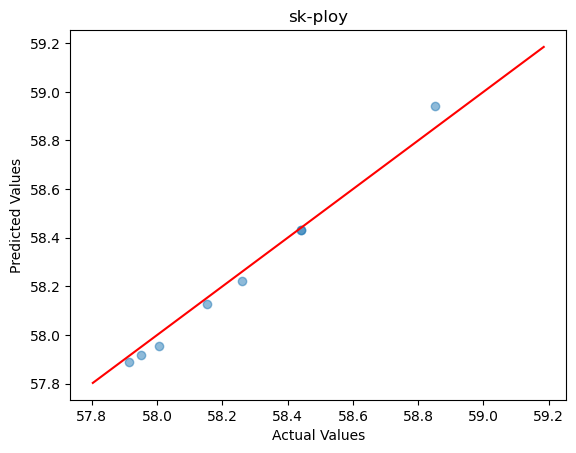
R2 score: 0.9801750123259995
Mean Squared Error: 0.0017544612190334443
Mean Absolute Error: 0.03380088277668314
Dataset38 Neural Network
The same 7-layer hidden neural network model used in the previous article was applied, and the prediction accuracy on the test set is shown in the figure below:
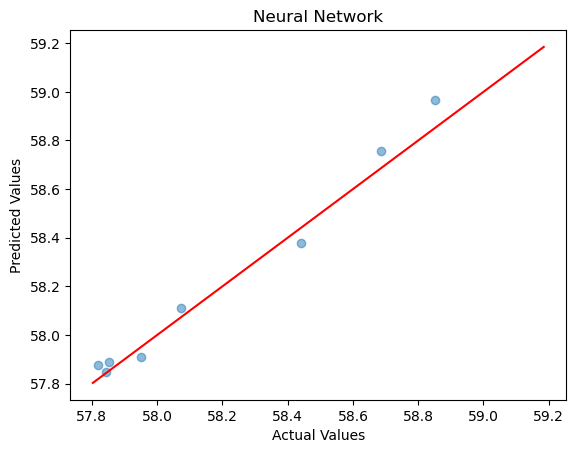
R2 score: 0.974916787662089
Mean Squared Error: 0.0037280149
Mean Absolute Error: 0.05290556
Other Datasets of Different Sizes
We also investigated datasets of various sizes. Ultimately, we plotted the R² scores of all datasets across different models, as shown in the figure below:
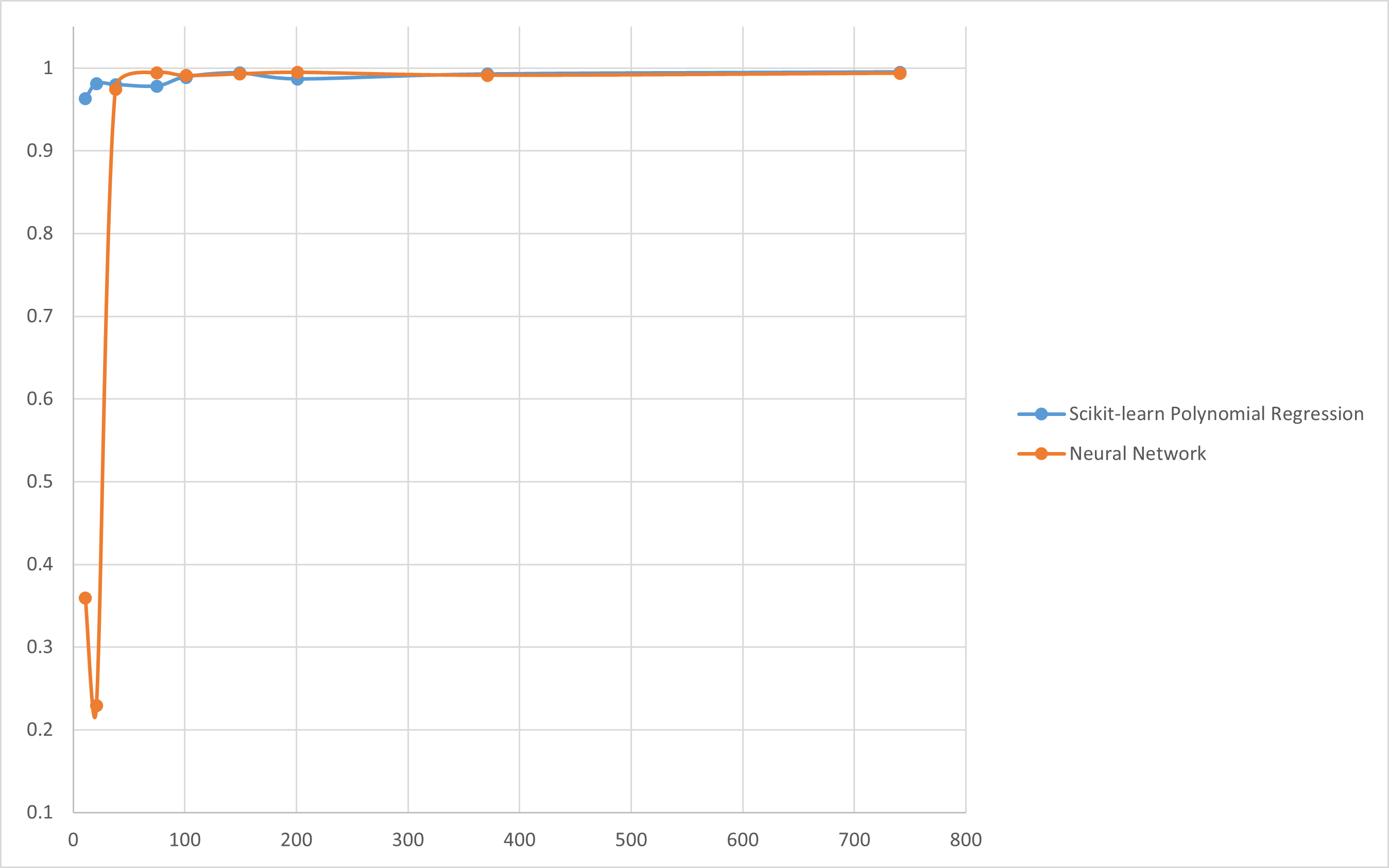
Conclusion
It is evident that when the dataset is relatively small, the accuracy of polynomial regression significantly exceeds that of the neural network model. This is because neural networks typically require a larger dataset; for example, with 11 data points and a 0.2 ratio for the test set, only 8 data points are available for training, making it difficult for the neural network to capture the non-linearity of the 𝐷−𝑇 relationship. Polynomial regression, on the other hand, is less affected by the dataset size.
As the dataset size increases, the accuracy of the neural network also reaches comparable levels.
In the next chapter, we plan to study using two parameters as variables.
